Simple random sampling can sometimes be impractical or inefficient when working with large populations. This is where systematic sampling becomes a valuable alternative for researchers and data analysts. This sampling technique is a probability-based approach that involves selecting elements from the target population at regular intervals, making it more streamlined than random sampling for large groups.
In systematic random sampling, you begin by listing the entire population and then selecting a starting point randomly. From there, you choose every nth individual, ensuring that every member of the population has an equal chance of being selected. This method is especially useful when you have access to a complete list of the population but lack the resources to conduct a fully random sample.
While systematic sampling offers efficiency, it may introduce bias if there is a hidden pattern in the data. Unlike cluster sampling and stratified sampling, where the sample may be divided into specific subgroups or clusters, systematic sampling assumes that the population is evenly distributed, which might not always be the case. Despite this, it remains an effective way to gather data when dealing with large, well-organized populations.
Types of Systematic Sampling
Systematic sampling is a sampling method in which sample elements are selected at regular intervals from a population of interest. This type of sampling is often preferred for its simplicity and efficiency, especially when working with large populations. There are three main types of systematic sampling methods:
- Systematic Random Sampling
- Linear Systematic Sampling
- Circular Systematic Sampling
Each of these techniques has its own advantages and may be used depending on the size of the population and the goals of the research.
Systematic Random Sampling
Systematic Random Sampling is a probability sampling method where researchers select a random starting point in the population and then choose every nth element from that point.
For example, if you’re sampling from a total population of 1,000 and need a sample size of 100, you would divide the population by the sample size to get the sampling interval (n = 10) and select every 10th individual.
This method reduces sampling bias and ensures that each random subset of the population is representative of the population. It’s a widely-used sampling procedure compared to other sampling methods like convenience sampling or quota sampling.
Linear Systematic Sampling
In Linear Systematic Sampling, elements are selected following a linear path through the population. The sampling process involves choosing a random starting point and selecting every nth element, similar to Systematic Random Sampling.
However, unlike Circular Systematic Sampling, this method does not loop back to the beginning after reaching the end of the population list. It works well when the size of the population is fixed and easily divisible. This form of systematic sampling is commonly used in statistical sampling and spatial sampling applications.
Circular Systematic Sampling
Circular Systematic Sampling is similar to Linear Systematic Sampling, but instead of stopping at the end of the list, it wraps around to the beginning. This method is useful when the population list is arranged in a circular or repeating pattern.
After selecting the initial random starting point, Circular Systematic Sampling continues by cycling through the population list, ensuring that every element has an equal chance of selection.
This technique helps minimize sampling bias that might occur due to the way systematic sampling is structured in linear approaches. It’s especially effective for populations that repeat or cycle.
By understanding these sampling methods, researchers can perform systematic sampling in a way that best fits their study design and sampling approach. Although systematic sampling has advantages in terms of simplicity and speed, researchers should always consider whether it is the most appropriate choice compared to other sampling techniques like stratified random sampling, cluster sampling, or multistage sampling to ensure the most accurate and unbiased results.
When to Use Systematic Sampling
Systematic sampling is a proper probability-based technique that can be implemented when simple random sampling is not feasible or practical. This method is particularly appropriate in the following situations:
Order of the Population
The order of the population refers to the arrangement or sequence of elements in the sampling frame. Sometimes, the population may have a natural or inherent order relevant to the research objectives. This order could be based on time, space, alternating characteristics, or any other meaningful pattern.
When the population has a relevant order, systematic sampling can be a particularly useful technique. By selecting elements from the ordered list at regular intervals, systematic sampling can leverage the population’s structure to obtain a representative sample efficiently.
Alternating list example
If a company wanted to survey an equal number of male and female employees and had a list of all employees alternating between male and female, systematic sampling could be used to easily select a balanced gender sample by picking a random start point and sampling at an interval that maintains the alternating pattern.
Cyclically ordered list example
Suppose a manufacturer wanted to inspect products coming off an assembly line that runs Monday through Friday. Using systematic sampling, they could randomly select a day to start and then sample every fifth day. This would ensure they inspect products made on different days throughout the cycle.
Systematic Sampling without a Population List
In some research scenarios, a complete population (sampling frame) list may not be available. However, systematic sampling can still be employed if the population elements can be accessed in some order or sequentially.
Research example
An ecologist wants to estimate the number of oak trees in a 100-acre forest. Rather than counting every tree, she could start at a random point, walk in a straight line, and sample every 50th tree encountered. Multiplying the sampled trees by 50 would provide an estimate for the whole forest.
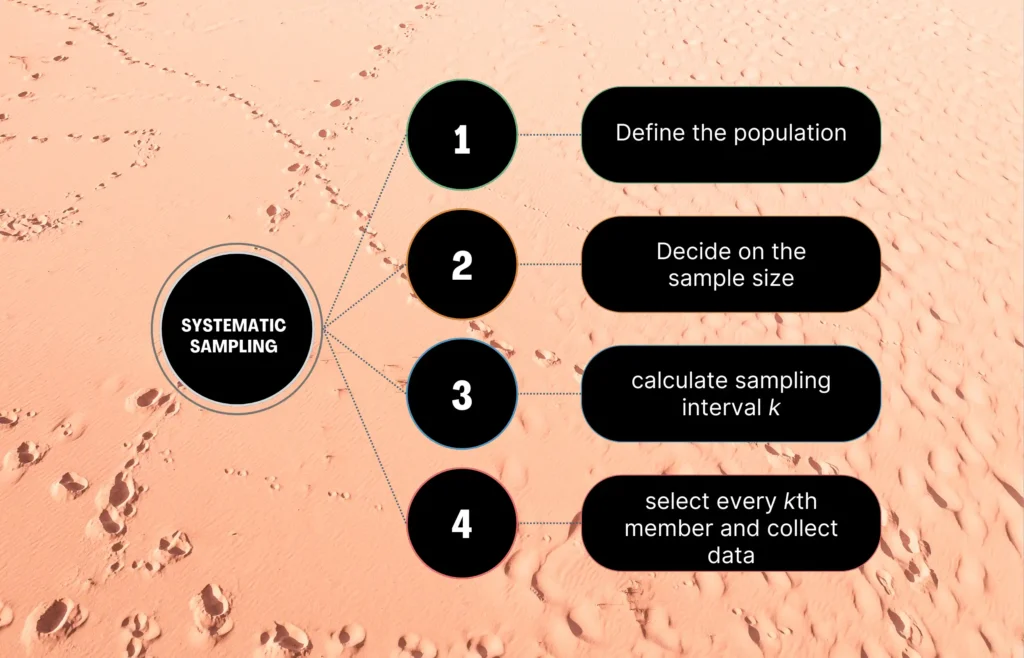
Steps for Implementing Systematic Sampling
Systematic sampling is a probability sampling method in which elements are selected from an ordered population at a regular interval. This interval, known as the sampling interval (k), is calculated by dividing the population size (N) by the desired sample size (n). The process starts by randomly selecting a starting point between 1 and k and then selecting every kth element from that point onward until the desired sample size is reached.
Implementing systematic sampling involves four key steps:
Step 1: Define your population
The first step in systematic sampling is defining the population you want to study. This involves specifying an element’s characteristics to be included in the population. For example, if you’re studying customer satisfaction at a particular store, your population might be all customers who purchased within the last month.
It’s important to ensure that your population definition is clear, specific, and aligned with your research objectives. A well-defined population helps ensure that your sample is representative and that your results can be generalized to the intended population.
Step 2: Decide on your sample size
Next, you must determine the number of elements you want to include in your sample. The sample size depends on various factors, such as the level of precision required, the variability of the population, and the resources available for the study.
Statistical formulas and techniques calculate the optimal sample size based on these factors. Larger sample sizes generally lead to more precise estimates and require more resources. When deciding on your sample size, it’s important to strike a balance between precision and feasibility.
Step 3: Calculate sampling interval k
The sampling interval (k) is the gap between each selected element in the ordered population. To calculate k, you divide the population size (N) by the desired sample size (n):
k = N / n
For example, if you have a population of 1000 customers and want a sample of 100, your sampling interval would be:
k = 1000 / 100 = 10
This means that you will select every 10th customer from the ordered list.
Step 4: Select the sample and collect data
With your population defined, sample size determined, and sampling interval calculated, you can select your sample and collect data.
First, choose a random starting point between 1 and k. This ensures that the starting point is not biased and that every element has an equal chance of being selected. You can use a random number generator or any other unbiased method to select the starting point.
Let’s say your randomly selected starting point is 7. This means you will select the 7th element in the ordered population as your first sample element.
From there, you add the sampling interval (k) to the starting point to determine the next element to be included in the sample. In our example, with a starting point of 7 and a sampling interval of 10, you would select the 7th, 17th, 27th, 37th, and so on until you reached your desired sample size of 100.
Once you have selected your sample, you can collect data using your chosen methods (surveys, observations, experiments, etc.).